Prozentrechnungen sind für Sie schwierig? Dinge wie das Berechnen von Rabatten, Steuern oder Trinkgeldern können schwierig sein, insbesondere bei großen Zahlen. Unser Online-Prozentrechner löst diese Probleme schnell und richtig.
Er ist einfach zu bedienen und funktioniert für alle Arten von Berechnungen. Egal, ob Sie einkaufen, die Mehrwertsteuer berechnen oder sich über Prozente informieren, mit diesem Tool wird alles zum Kinderspiel. Es spart Zeit, vermeidet Fehler und gibt Ihnen schnell und unkompliziert Antworten.
Was ist ein Prozentrechner?
Ein Prozentrechner hilft Ihnen, die Prozentberechnung schnell und einfach durchzuführen. Prozente zeigen Teile eines Ganzen und werden mit dem Symbol % geschrieben. Zum Beispiel, wenn Sie 10 € von 50 € sparen, zeigt der Rechner, dass Sie 20 % gespart haben. Er wandelt auch Brüche, Dezimalzahlen oder Verhältnisse in Prozente um, damit sie leicht verständlich sind.
Du kannst diesen Rechner für Prozentberechnungen nutzen, um Rabatte, Steuern oder Änderungen von Beträgen fehlerfrei zu ermitteln. Er vereinfacht die Prozentrechnung, beispielsweise durch das Verschieben des Dezimalpunkts, um durch 100 zu teilen. Egal ob beim Einkaufen, Planen oder Lernen – er spart Zeit und liefert klare Ergebnisse.
Beispiele für Prozentrechnungen
Beispiel 1
Was sind 25 % von 200?
Eine Firma stellt 200 Produkte her. Wenn wir 25 % davon berechnen wollen, wie viele sind das?
Lösung
- Was bedeutet 25 %?
25 % bedeutet 25 von 100. - Wie berechnen wir das?
Um 25 % von 200 zu finden, multiplizieren wir 200 mit 0,25 (weil 25 % = 0,25 ist). - Rechnung
200×0,25 = 50
Antwort
25 % von 200 Produkten sind 50 Produkte. Das bedeutet, dass 25 % des Gesamtbetrags 50 sind.
Beispiel 2
Wie viel Prozent sind 50 von 200?
Von 100 Gegenständen werden 50 verwendet. Wie viel Prozent sind das?
Lösung
- Was bedeutet 25 %?
Wir möchten wissen, wie viel 50 als Prozentsatz von 100 ist. - Wie berechnen wir das?
Um den Prozentsatz zu berechnen, teilen wir 50 durch 100 und multiplizieren dann mit 100:
50÷100×100 - Rechnung
50÷100= 0,5, und 0,5×100 = 50
Antwort
50 sind 50% von 100. Das bedeutet, die Hälfte von 100 sind 50%.
Beispiel 3
Wie addiert oder subtrahiert man Prozentsätze?
Du möchtest eine Jacke kaufen, die €100 kostet. Der Laden gibt dir 20 % Rabatt, aber danach musst du noch 10 % Steuer zahlen. Wie viel kostet die Jacke am Ende?
Lösung
- Rabatt berechnen
20 % von €100 sind
20%×100 =€20.
Den Rabatt abziehen
100−20= €80. - Steuer berechnen
10 % von €80 sind
10%×80= €8.
Die Steuer hinzufügen
€80+€8= €88.
Antwort
Die Jacke kostet €88, nachdem der Rabatt und die Steuer berechnet wurden.
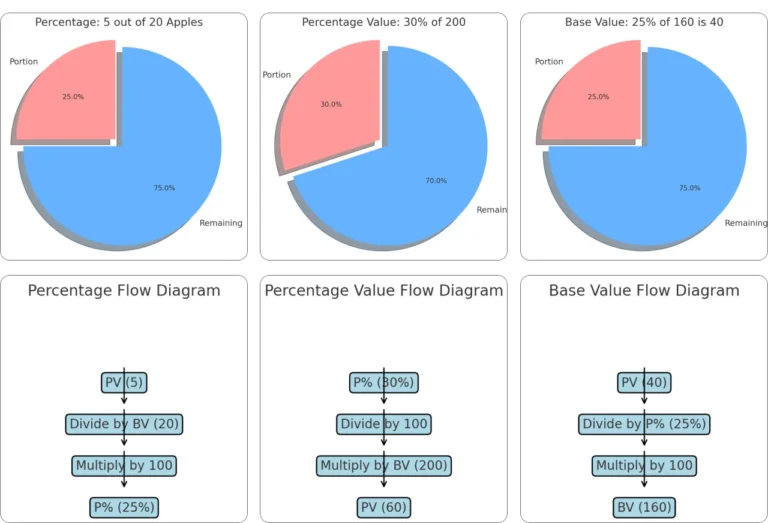
Kernformeln der Prozentrechnung
Die Prozentrechnung basiert auf drei einfachen Begriffen: Prozentsatz (P), Prozentwert (W) und Grundwert (G). Diese sind die grundlegenden Bausteine, um Fragen zu lösen, wie z. B. Rabatte, Steuern oder das Verhältnis zwischen zwei Zahlen zu berechnen.
Stellen Sie sich eine Pizza vor, bei der jedes Stück den Prozentsatz (P) darstellt, die Größe des Stücks der Prozentwert (W) ist und die ganze Pizza der Grundwert (G). So wird deutlich, wie Prozente Teile mit dem Ganzen verbinden.
Hier sind die Formeln für diese drei Begriffe
Konzept | Formel | Beispiel |
Prozentsatz (P) | P= W/G×100 | 50/200×100= 25% |
Prozentwert (W) | W= P×G/100 | 25×200/100= 50 |
Grundwert (G) | G= W/P×100 | 50/25×100= 200 |
Diese Formeln sind nicht nur für die Schule nützlich, sondern auch im Alltag. Zum Beispiel können Sie berechnen, wie viel 15 % Ihres Gehalts ausmachen, oder wie stark ein Preis gestiegen ist. Das Verständnis dieser Konzepte und Formeln macht die Prozentrechnung praktisch und einfach im täglichen Leben anwendbar.
Prozentsatz (P)
Die Prozentsatz-Formel ist hilfreich, wenn Sie herausfinden möchten, wie viel ein Wert im Vergleich zu einem anderen in Prozent ausmacht. Zum Beispiel können Sie damit berechnen, wie viel von Ihren Ersparnissen Sie ausgegeben haben, wie weit Sie in einer Aufgabe gekommen sind oder wie viel von einem Ziel erreicht wurde.
Die Formel für den Prozentsatz (P)
P= W/G×100
Dabei gilt
- P= Prozentsatz
- W= Der gemessene Teil
- G= Der Gesamtwert
Beispiel
Sarah liest ein Buch mit 300 Seiten und hat bisher 90 Seiten geschafft. Um herauszufinden, wie viel Prozent des Buches sie gelesen hat, teilen wir die gelesenen Seiten durch die Gesamtseiten und multiplizieren mit 100.
P= 90/300×100= 0,3×100= 30%
Antwort
Sarah hat 30% ihres Buches gelesen.
Prozentwert (W)
Die Prozentwert-Formel hilft Ihnen, herauszufinden, wie viel ein Prozentsatz von etwas in tatsächlichen Zahlen beträgt. Sie können sie verwenden, um Rabatte zu berechnen, den Steuerbetrag herauszufinden oder zu sehen, wie viel von Ihrem Budget Sie ausgegeben haben.
Die Formel für den Prozentwert (W)
W =P/100×G
Dabei gilt
- W = Der Prozentwert (der Betrag, den Sie berechnen möchten)
- P= Der Prozentsatz
- G= Der Gesamtwert (Grundwert)
Beispiel
Ali möchte ein Handy kaufen, das €800 kostet, und der Laden bietet 25 % Rabatt an. Um herauszufinden, wie viel Ali spart, verwenden wir die Formel:
W= 25/100×800= 0,25×800= 200
Antwort
Ali spart €200 beim Kauf des Handys.
Grundwert (G)
Die Grundwert-Formel hilft Ihnen, den gesamten oder ursprünglichen Betrag zu finden, wenn Sie bereits einen Teil davon (Prozentwert) und den Prozentsatz kennen. Dies ist nützlich, um den ursprünglichen Preis vor einem Rabatt herauszufinden, Ihr Gesamteinkommen zu berechnen, wenn Sie wissen, wie viel Sie für die Miete zahlen, oder den Gesamtbetrag zu berechnen, wenn nur ein Teil bekannt ist.
Die Formel für den Grundwert (G)
G= W/P×100
Dabei gilt
- G = Grundwert (der gesamte oder ursprüngliche Betrag)
- W = Prozentwert (der bekannte Teil)
- P = Prozentsatz
Beispiel
Emma zahlt €500 Miete, was 40 % ihres gesamten Einkommens entspricht. Um herauszufinden, wie viel sie insgesamt verdient, verwenden wir die Formel:
G= 500/40×100= 12,5×100= 1250
Antwort
Emmas Gesamteinkommen beträgt €1.250.
Verschiedene Prozentrechner
Prozentrechner sind nützliche Werkzeuge, die alltägliche Mathematik einfach machen. Sie sparen Zeit und helfen dabei, Fehler zu vermeiden. Egal ob Sie Zahlen vergleichen, Veränderungen nachverfolgen oder Ihr Budget planen, diese Rechner liefern schnelle und genaue Antworten. Unten finden Sie sechs Arten von Prozentrechnern und deren Anwendungen.
Rechnertyp | Anwendungsfall | Beispiel |
Prozentuale Erhöhung-Verringerung | Veränderung en von Werten im Laufe der Zeit verfolgen | Preis von 100 € auf 120 € erhöht = 20% Erhöhung |
Mehrwertsteuer- Prozent | Mehr wertsteuer hinzufügen entfernen | Netto 100 € + 19% MwSt = Brutto 119 € |
Rabatt-prozentsatz | Ersparnisse während des Verkaufs berechnen | 50 € mit 10% Rabatt = 45 € |
Gewinn/Verlust-prozentsatz | Geschäftsgewinn und -verlust berechnen | 500 € Kosten, 600 € Verkauf = 20% Gewinn |
Prozentuale-Differenz | Zwei Werte vergleichen, um die Differenz zu finden | Differenz zwischen 80 und 120 = 40/100×100 = 40% |
Rechner für prozentuale Erhöhung oder Verringerung
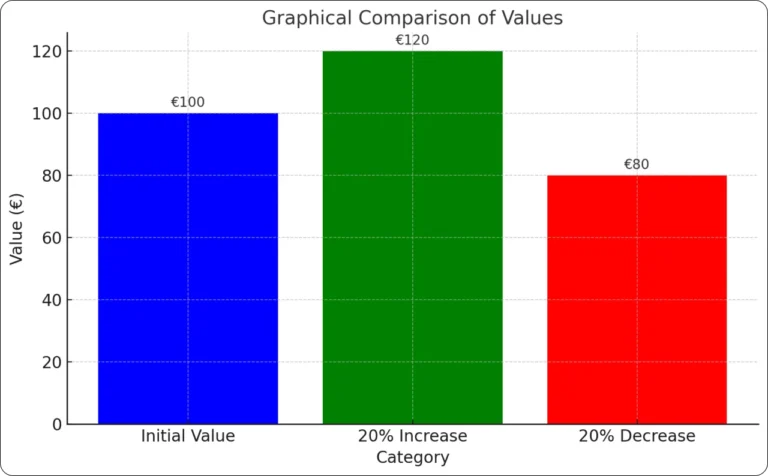
Die prozentuale Veränderung ist eine einfache Methode, um zu messen, wie viel etwas im Vergleich zu seinem ursprünglichen Wert gestiegen oder gesunken ist. Sie hilft Ihnen, Änderungen bei Preisen, Ausgaben, Einkommen oder Leistungen nachzuverfolgen. Egal, ob es sich um eine Preiserhöhung oder einen Rabatt handelt, die prozentuale Veränderung zeigt Ihnen die Differenz klar und deutlich.
Formel
Prozentuale Vera¨nderung=Neuer Wert−Urspru¨nglicher Wert/ Urspru¨nglicher Wert×100
- Wenn das Ergebnis positiv ist, bedeutet das eine prozentuale Erhöhung.
- Wenn das Ergebnis negativ ist, bedeutet das eine prozentuale Verringerung.
Beispiel 1
Prozentuale Erhöhung
Ein Unternehmen hat letztes Jahr 50.000 € Umsatz gemacht. Dieses Jahr sind es 60.000 €. Um die prozentuale Erhöhung zu berechnen
Schritt 1: Formel verwenden
Prozentuale Veränderung= Neuer Wert−Urspru¨nglicher Wert/ Urspru¨nglicher Wert×100
Schritt 2: Werte einsetzen
Prozentuale Veränderung= 60.000−50.000×100/ 50.000
Prozentuale Veränderung= 10.000×100/ 50.000= 20%
Antwort
Der Umsatz ist um 20 % gestiegen.
Beispiel 2
Prozentuale Verringerung
Ein Telefon, das ursprünglich 800 € gekostet hat, ist jetzt für 640 € im Angebot. Um die prozentuale Verringerung zu berechnen
Schritt 1: Formel verwenden
Prozentuale Veränderung= Neuer Wert−Urspru¨nglicher/ WertUrspru¨nglicher Wert×100
Schritt 2: Werte einsetzen
Prozentuale Veränderung= 640−800×100/ 800= −20%
Antwort
Der Preis ist um 20 % gesunken.
Mehrwertsteuerrechner (Netto zu Brutto)
Die Mehrwertsteuer (MWSt.) ist eine Steuer, die in Deutschland auf Waren oder Dienstleistungen erhoben wird. Sie beträgt entweder 19 % (Regelsatz) oder 7 % (ermäßigter Satz). Egal, ob Sie den Preis inklusive MWSt. (Brutto) oder ohne MWSt. (Netto) berechnen möchten, ein MWSt.-Rechner macht es schnell und einfach – für Unternehmen und Verbraucher.
Formeln zur Berechnung der Mehrwertsteuer
1. Um den Bruttobetrag (mit MWSt.) zu berechnen
Brutto= Netto×(1+MWSt. Satz/100)
2. Um den Nettobetrag (ohne MWSt.) zu berechnen
Netto= Brutto/ 1+MWSt. Satz/ 100
3. Um die MWSt. zu berechnen
MWSt.= Brutto−Netto
Beispiel 1
Brutto zu Netto
Ein Produkt wird für 119 € verkauft, inklusive 19 % MWSt. Um den Preis ohne MWSt. zu berechnen
Netto= 119/ 1+19/ 100 =>119/ 1.19 =>100
Antwort
Der Nettopreis beträgt 100 €, und die MWSt. beträgt 19 €.
Beispiel 2
Netto zu Brutto
Der Nettopreis eines Produkts beträgt 100 €, und es gilt ein MWSt.-Satz von 7 %. Um den Preis inklusive MWSt. zu berechnen:
Brutto=100×(1+7/ 100) =>100×1.07 =>107
Antwort
Der Bruttopreis beträgt 107 €, und die MWSt. beträgt 7 €.
Rabatt- und Sparrechner
Rabatte sind eine großartige Möglichkeit, Geld zu sparen, indem der ursprüngliche Preis eines Produkts oder einer Dienstleistung reduziert wird. Sie finden Rabatte oft bei großen Verkäufen, Sonderaktionen oder als Belohnung für eine schnelle Zahlung von Rechnungen. Zu wissen, wie man Rabatte berechnet, hilft Ihnen nicht nur, Ihre Ausgaben besser zu planen, sondern macht Sie auch zu einem clevereren Käufer.
Wie berechnet man Rabatte?
1. Rabatt berechnen
Rabatt= Urspru¨nglicher Preis×Rabattprozentsatz/100
2. Rabatt vom ursprünglichen Preis abziehen
Endpreis= Urspru¨nglicher Preis−Rabatt
Beispiel
Stellen Sie sich vor, Sie möchten eine Jacke kaufen, die €200 kostet, und das Geschäft bietet einen Rabatt von 25 % an.
Schritt 1
Rabatt berechnen
200×0,25=50
Sie sparen €50.
Schritt 2
Rabatt vom ursprünglichen Preis abziehen:
200−50=150
Der Endpreis beträgt €150.
Antwort
Der Rechner zeigt, dass Sie €50 sparen, und der Endpreis beträgt €150.
Prozentrechner für Gewinn und Verlust
Zu wissen, wie viel Gewinn oder Verlust Sie machen, ist wichtig, um kluge finanzielle Entscheidungen zu treffen. Egal, ob Sie ein Geschäft führen, investieren oder Ihr Geld verwalten, diese Berechnungen helfen Ihnen zu verstehen, wie gut Sie abschneiden. Diese Prozentaufgabe ist perfekt, um Kosten, Verkäufe und Einnahmen zu vergleichen.
Formeln für Gewinn und Verlust
1. Gewinn
Gewinn= Verkaufspreis−Kostenpreis
2. Gewinnmarge
Gewinnmarge= Gewinn/ Verkaufspreis×100
3. Gewinnprozentsatz
Gewinnprozentsatz= Gewinn/ Kostenpreis×100
4. Verlust
Verlust= Kostenpreis−Verkaufspreis
5. Verlustprozentsatz
Verlustprozentsatz=Verlust/ Kostenpreis×100
Beispiel 1
Sie kaufen einen Artikel für 100 € und verkaufen ihn für 150 €.
Schritt 1
Gewinn berechnen
Gewinn= 150−100= 50
Schritt 2
Gewinnmarge berechnen
Gewinnmarge= 50/ 150×100= 33,33%
Schritt 3
Gewinnprozentsatz berechnen
Gewinnprozentsatz= 50/ 100×100= 50%
Antwort
Sie haben einen Gewinn von 50 € gemacht. Ihre Gewinnmarge beträgt 33,33%, und Ihr Gewinnprozentsatz beträgt 50%.
Beispiel 2
Sie kaufen einen Artikel für 100 €, verkaufen ihn aber für 80 €.
Schritt 1
Verlust berechnen
Verlust= 100−80= 20
Schritt 2
Verlustprozentsatz berechnen
Verlustprozentsatz= 20/ 100×100= 20%
Antwort
Sie haben einen Verlust von 20 €, und Ihr Verlustprozentsatz beträgt 20%.
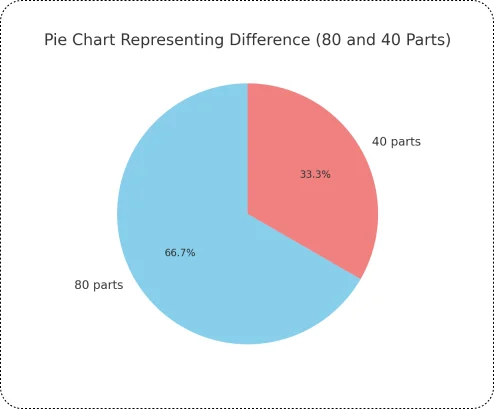
Rechner für prozentuale Unterschiede
Die Prozentdifferenz zeigt, wie viel zwei Zahlen prozentual voneinander abweichen. Im Gegensatz zur prozentualen Veränderung, die verfolgt, wie sich eine Zahl im Laufe der Zeit verändert, vergleicht die Prozentdifferenz zwei Zahlen unabhängig von ihrer Reihenfolge. Das macht sie nützlich für den Vergleich von Preisen, Testergebnissen oder Messwerten.
Formel für die Prozentdifferenz
Prozentdifferenz= Wert 1−Wert 2/ Durchschnitt aus Wert 1 und Wert 2×100
Beispiel
Zwei Smartphones kosten 750 € und 850 €. Um die Prozentdifferenz zu berechnen
1. Berechnen Sie die Differenz
850−750= 100
2. Berechnen Sie den Durchschnitt
750+850/ 2= 800
3. Berechnen Sie die Prozentdifferenz:
100/ 800×100= 12,5%
Antwort
Die Prozentdifferenz zwischen den beiden Smartphones beträgt 12,5%.
Wie funktioniert der Prozentrechner?
Ein Prozentsatzrechner ist ein einfach zu bedienendes Werkzeug, das Ihnen hilft, Prozentprobleme schnell zu lösen. Egal, ob Sie einen Rabatt berechnen, die Mehrwertsteuer ermitteln, Gewinn und Verlust überprüfen oder Werte vergleichen möchten – dieses Tool macht es Ihnen leicht. Mit der Prozentberechnung online können Sie Zeit sparen und genaue Ergebnisse erhalten, ohne selbst rechnen zu müssen. So funktioniert es.
So verwenden Sie es
1. Prozentsatz eingeben
Geben Sie den Prozentsatz ein, den Sie berechnen möchten, z. B. 15 % für einen Rabatt.
2. Wert eingeben
Fügen Sie den Basiswert hinzu, z. B. 1.200 € für den Preis eines Produkts.
3. Ergebnis ansehen
Das Tool zeigt Ihnen sofort die Antwort an, z. B. den Rabattbetrag oder den Gesamtpreis.
Beispiel
Sie möchten ein Trinkgeld von 20 % für eine Restaurantrechnung von 50 € geben.
- Geben Sie 20 % in das Prozentfeld ein.
- Geben Sie 50 € in das Wertfeld ein.
- Das Tool zeigt Ihnen das Ergebnis: 10 €.
Antwort
Sie sollten ein Trinkgeld von 10 € geben.
Erweiterte Prozentkonzepte
Prozentsätze sind nicht nur für Rabatte oder einfache Mathematik gedacht. Sie werden auch verwendet, um kompliziertere Probleme zu lösen. Egal, ob Sie mit Finanzen arbeiten, Daten analysieren oder reale Probleme lösen – fortgeschrittene Prozentkonzepte können Ihnen helfen, bessere Lösungen zu finden.
Umwandlung von Prozentsätzen in Brüche
Das Umwandeln von Prozentsätzen in Brüche ist einfach und nützlich – sei es in der Mathematik, beim Kochen oder im Alltag. Egal, ob Sie einem Rezept folgen, Finanzberichte lesen oder etwas messen, diese Methode macht Zahlen einfacher. Mit der Prozentberechnung online wird es noch schneller und genauer. So funktioniert es.
Schritte zur Umwandlung von Prozentsätzen in Brüche
1. Prozentsatz in Dezimalzahl umwandeln
Teilen Sie den Prozentsatz durch 100.
Beispiel.
75%÷100= 0,75
2. Als Bruch schreiben
Schreiben Sie die Dezimalzahl als Zähler (obere Zahl) und 1 als Nenner (untere Zahl).
Beispiel:
= 0,75/ 1
3. Dezimalzahl entfernen
Multiplizieren Sie sowohl den Zähler als auch den Nenner mit 10, 100 oder mehr, um die Dezimalzahl zu entfernen.
Beispiel: Für 0,75 multiplizieren Sie mit 100:
0,75/ 1×100/ 100= 75/ 100
4. Bruch vereinfachen
Teilen Sie Zähler und Nenner durch ihre größte gemeinsame Zahl.
Beispiel:
75/ 100= 3/4
Beispiel: Anwendung im Alltag
Sie folgen einem Rezept, das 50 % einer Tasse Zucker verlangt, aber Ihr Messbecher zeigt nur Brüche. So wandeln Sie 50 % in einen Bruch um.
1. In Dezimalzahl umwandeln
50÷100= 0,5
2. Als Bruch schreiben
= 0,5/1
3. Dezimalzahl entfernen
Multiplizieren Sie mit 10:
0,5/1×10/10 =>5/10
4. Vereinfachen
Teilen Sie durch 5:
5/10 =>1/2
Antwort
50 % entspricht 1/2, also benötigen Sie eine halbe Tasse Zucker.
Zusammengesetzte Prozentberechnungen
Zusammengesetzte Prozentberechnungen werden verwendet, um zu berechnen, wie sich Zahlen im Laufe der Zeit ändern, wenn jede Änderung auf der vorherigen aufbaut. Im Gegensatz zu einfachen Prozentsätzen, bei denen jede Änderung separat betrachtet wird, berücksichtigen zusammengesetzte Prozentsätze, wie sich Änderungen summieren.
Das macht sie ideal für Dinge wie finanzielles Wachstum, Bevölkerungszunahmen oder die Ermittlung des Endpreises nach mehreren Rabatten. Mit der Prozentberechnung online können Sie diese Berechnungen ganz einfach durchführen.
Wie es funktioniert?
1. Grundidee verstehen
Jede prozentuale Änderung baut auf dem vorherigen Ergebnis auf.
3. Den Rechner nutzen
Geben Sie den Anfangswert, den Prozentsatz und die Anzahl der Wiederholungen ein. Der Rechner erledigt den Rest.
2. Formel verwenden
Für Wachstum: Endwert=Anfangswert×(1+Rate/100)n
Rate:
Der Prozentsatz des Wachstums oder der Änderung.n: Anzahl der Wiederholungen der Änderung.
Beispiel 1: Finanzielles Wachstum
Sie investieren 1.000 € mit einer jährlichen Wachstumsrate von 5 % für 3 Jahre.
Formel anwenden
Endwert=1.000×(1+5/100)3
= 1.000 × (1,05)^3
= 1.157,63
Antwort
Nach 3 Jahren wächst Ihre Investition auf 1.157,63 €.
Beispiel 2: Mehrere Rabatte
Ein Geschäft bietet einen Rabatt von 20 %, gefolgt von weiteren 10 % auf einen Artikel für 500 €.
- Erster Rabatt:
= 500×(1−20/100)
= 500×0,8
= 400
- Zweiter Rabatt:
= 400×(1−10/100)
= 400×0,9
= 360
Antwort
Nach beiden Rabatten beträgt der Endpreis 360 €.
Tipps für genaue Prozentberechnungen
Genaue Prozentberechnungen sind wichtig, um alltägliche Probleme zu lösen, wie z. B. den Umgang mit Geld, das Messen von Dingen oder das Finden von Rabatten beim Einkaufen. Diese Tipps helfen Ihnen, Fehler zu vermeiden und Berechnungen mit Tools wie Pocket Percentage Calculation einfacher zu machen.
Häufige Fehler, die vermieden werden sollten
Beim Arbeiten mit Prozentsätzen können selbst kleine Fehler zu falschen Ergebnissen führen. Hier sind einige häufige Fehler, die Sie vermeiden sollten, besonders bei der Lösung von Prozentrechnungs-Wortaufgaben.
1. Die Frage falsch verstehen
Manchmal ist es unklar, ob sich der Prozentsatz auf das Gesamte oder nur auf einen Teil bezieht. Lesen Sie die Aufgabe sorgfältig durch und teilen Sie sie in einfache Schritte auf.
2. Das Umrechnen von Einheiten vergessen
Achten Sie darauf, dass alle Werte die gleichen Einheiten haben. Zum Beispiel sollten Gramm in Kilogramm oder Stunden in Minuten umgerechnet werden, wenn nötig.
3. Nicht durch 100 teilen
Denken Sie daran, dass Prozentsätze keine ganzen Zahlen sind. Teilen Sie sie durch 100, um sie richtig zu verwenden. Zum Beispiel sollte 25 % als 0,25 geschrieben werden.
4. Zu früh runden
Runden Sie Zahlen nicht mitten in der Berechnung. Warten Sie bis zum Schluss, um Fehler zu vermeiden.
5. Die Antwort nicht überprüfen
Das Lösen von Prozentrechnungs-Wortaufgaben erfordert oft mehrere Schritte. Überprüfen Sie immer Ihre Arbeit, um sicherzustellen, dass alles stimmt.
Schnelle Abkürzungen und Eselsbrücken
Prozentrechnungen müssen nicht schwierig sein. Mit einfachen Abkürzungen und Tricks können Sie Probleme schneller lösen und leichter verstehen, wie Prozentrechnungen funktionieren. Hier sind ein paar schnelle Tipps, um Ihre Berechnungen zu vereinfachen.
1. Abkürzungen für schnelle Berechnungen.
2. 10 %-Regel.
Um 10 % einer Zahl zu finden, verschieben Sie einfach das Komma um eine Stelle nach links.
Beispiel: 10 % von 250 sind 25,0.
3. 5 % oder 15 % schnell finden.
Für 5 % nehmen Sie 10 % und teilen diese durch zwei. Für 15 % addieren Sie 10 % und 5 %.
Beispiel: 5 % von 200 sind 10.
4. Verdoppeln oder Halbieren.
Für Prozentsätze wie 20 % oder 50 % ist Verdoppeln oder Halbieren sehr einfach.
Beispiel: 50 % von 400 sind 400÷2= 200.
5. Schritt-für-Schritt für mehrere Prozentsätze.
Bei Aufgaben mit zwei oder mehr Prozentsätzen (z. B. 20 % Rabatt und dann weitere 10 %) rechnen Sie Schritt für Schritt.
Abkürzung | Erklärung | Beispiel |
10% Regel | Verschieben Sie das Komma um eine Stelle nach links | 10% of 250 = 25 |
50%= Hälfte | Durch 2 teilen | 50% of 100 = 50 |
5% = Hälfte von 10% | 10 % berechnen und dann durch 2 teilen | 5% of 200 = 10 |
Baust-eine | Prozentsatz in kleine Schritte aufteilen | 30% = 10% + 10% + 10% |
Tricks, um Prozentsätze zu merken
1. “Prozent bedeutet von 100”
Teilen Sie Prozentsätze immer durch 100. Diese einfache Regel erklärt, wie Prozentrechnungen funktionieren, und hilft, Fehler zu vermeiden.
2. Halb, Viertel und Achtel-Regel.
50 % = Hälfte, 25 % = Viertel und 12,5 % = Achtel. Diese lassen sich leicht merken, um schnelle Schätzungen vorzunehmen.
3. 10 %-Schritte nutzen.
Teilen Sie Prozentsätze in 10 %-Schritte auf. Zum Beispiel sind 30 % einfach drei 10 %-Schritte.
Ressourcen zum Lernen von Prozentsätzen
Das Lernen von Prozentrechnungen kann mit den richtigen Hilfsmitteln einfach und sogar spaßig sein. Egal, ob Sie praktische Übungen oder detaillierte Anleitungen bevorzugen – diese Ressourcen helfen Ihnen dabei, Ihre Fähigkeiten Schritt für Schritt zu verbessern. Sie sind so gestaltet, dass Prozentrechnungen für alle leicht verständlich werden.
Interaktive Quizze und Übungsaufgaben
Möchten Sie Prozentrechnungen auf einfache Weise lernen? Probieren Sie unser unterhaltsames und einfaches Quiz-Tool aus! Es wurde entwickelt, um Ihnen Schritt für Schritt zu helfen, Ihre Fähigkeiten zu verbessern.
Egal, ob Sie schnelle Fragen wie „Was sind 30 % von 90?“ lösen oder an kniffligen Aufgaben arbeiten, unser Tool macht das Lernen von Prozenten effektiv und macht Spaß. Sie können sogar verstehen, wie Tools wie percentage calculator grades in realen Szenarien helfen können.
Herunterladbares E-Book zur Prozentrechnung
Ein E-Book zur Prozentrechnung ist eine großartige Möglichkeit, Schritt für Schritt Prozentrechnungen zu lernen. Diese E-Books bieten oft klare Erklärungen, Beispiele und sogar eine Prozentrechnungstabelle, die Ihnen hilft, Aufgaben einfach zu verstehen und zu lösen.
FAQ’s